Rating Climbs: a simple formula

Last post I reviewed some existing ratings for climbs. All fell short. With this in mind, I propose my own rating here.

First, a quick review of my rating philosophy:

1. For simplicity, the rating should be based on net climbing and distance.
2. For sufficiently gradual grades, the rider is assumed to be able to shift to remain in a comfort zone on the climb, and difficulty is then proportional to altitude gained.
3. Beyond a certain grade, climbing becomes much more difficult. It may be possible to construct bicycles which can climb steep grades relatively easily, but the rating is designed for a "typical" fit rider on a typical racing bicycle.

From the description, an obvious candidate for the rating is immediately self-evident for fans of polynomials:

rating = net climbing × (1 + [K × climbing / distance]^N)

The only question is then: what value of K, and what value of N?

First, K: K is the distance / climbing at which a climb is twice as steep as it would be were it more gradual, neglecting issues of added distance traveled (which we're not including in "climb difficulty"). When I'm riding, personally I find "really steep" kicks in at around 12%. Think Metcalf at this past Sunday's LiveStrong Challenge. But the key is that climbs with a high average grade typically vary a bit, or even more than a bit, about that average. So a rock-steady 12% average might be less difficult than the "typical" 12% average grade, which has sections at 15% or more, and others at a more modest (but still steep) 7%. So after playing around with ratings a bit and looking at climbs I know well, I determined a rate of climbing of 10% was a good number to use here. In other words, K = 10.

Next, there's the issue of N. N = 1 reduces to the formula used by Summerson (for infinite K). Honestly I don't think that does justice to really steep climbs like Filbert Street in San Francisco. Filbert gains only a bit over 20 meters, but it's a lot tougher than a 40 meter climb at 15%. So next I tried N = 2. That seemed to work well. N = 3 really kicks in the difficulty at steep grades, but didn't do enough for moderate grade roads.  To be honest, I was going to pick N = 3, but after experimenting with some local climbs, I went back to N = 2.

I plot the formula's result for grades up to 30%. Note this is difficulty per unit climbing, not unit distance traveled. To convert to grade you can use high school trigonometry:

grade = (climbing / distance) / √1 - (climbing / distance)²,

or equivalently

climbing / distance = grade / √1 + grade².

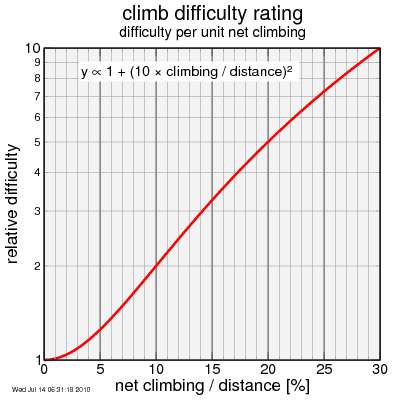Climbing difficulty per altitude gained
This seems to capture things fairly well. It says Filbert Street, the stiff portion of which gains around 18 meters @ 32% actual grade, corresponding to climbing / height = 30.5%, is equivalent to a 5% climb gaining around 150 meters. Well, difficulty on such a steep climb is hard to assess (for example, I might personally find 35% unclimbable), but for a quick-and-dirty rating, not too bad.

So there it is: my proposed formula for ranking the diffulty of climbs:

rating = net climbing × (1 + [10 × climbing / distance]²)

There's still one open question, however: how do I define a climb? Answer: a "climb" is a segment of road which has a higher climbing rating than any overlapping segment of road. What this implies is no "climb" should be rated lower than any subset of that climb. So suppose a climb starts gradually,then is steep for awhile, then levels out, like Metcalf Road.    One should be careful to consider using the steep portion rather than the absolute endpoints of the altitude-gaining segment for the rating.  More on that when I show some examples, but this is a bit of a point of weakness in the rating scheme versus one which used a detailed profile of the climb.  I'll make an attempt at such a rating system in a future post.

simple discount formula