CV Therapeutics Wins FDA Approval

CV Therapeutics (CVTX NASDAQ) and Astellas Pharma Inc announced on Friday that the U.S. Food and Drug Administration has approved Lexiscan (regadenoson), a heart imaging agent.

Astellas signed a license agreement with CV Therapeutics for the development and sale of the agent in July 2007.

CV Therapeutics, Astellas Heart-Monitor Drug Approved

stem and leaf plot maker

A Million Dollars for Solving a Math Problem -- Will the Winner Show Up?

The Clay Mathematics Institute has announced the winner of the 1 million dollar prize for the resolution of the Poincare conjecture, which is a conjecture in a branch of mathematics known as topology. The announcement was made this week by Dr. James Carlson, the President of the Clay Institute, that Dr. Grigoriy Perelman of St.Petersburg, Russia is the winner of this prize.

Dr. Perelman in 2006 received the prestigious Fields Medal but never claimed it. The New York Times, in an article, is wondering whether he will (or will not) claim the million dollar prize for solving a longstanding mathematics problem that was one of seven selected for the Millenium Awards by the Clay Institute, which is located in Cambridge, Massachusetts.

Interestingly, Dr. Perelman, 7 years ago, in 3 papers p! osted on the Internet, provided the solution to this math problem, which was posed in 1904 by Poincare. The news of his results quickly spread (at least in math circles) and he embarked on a whirlwind series of speaking engagements, only to return back to Russia and then resign from his post at the Steklov Institute of Mathematics. He stopped answering email messages and, in a sense, disappeared professionally.

According to The New York Times, several teams of mathematicians, using Dr. Perelman’s papers as a guide, completed a full proof of the conjecture in manuscripts hundreds of pages long, showing that Dr. Perelman was right.

The Clay Institute plans to hold a conference to celebrate the solution of the Poincaré conjecture on June 8 and 9 in Paris, France. Dr. Carlson was quoted as saying that Dr. Perelman will let him know in due time whether he will accept this pri! ze.

There are 6 other math problems left as Millen! nium Pro blems, so for those who are interested, you may find the list here. The solution of any of these will garner you a million dollars.

solve math problem

How to find slope intercept

Introduction:

     An area of surface that tends evenly towards top or down is called as slope. The slope of a line in the plane containing the x and y axes is generally represented by the letter m, and is defined as the change in the y coordinate divided by the corresponding change in the x coordinate, between two distinct points on the line. For finding slope intercept we need to know the following things.

Finding slope intercept form:

Slope intercepts form:

The standard form of a line i! s,

ax+by+c=0    

We can express the line as slope intercept form. The slope intercept form of a line is,

y=mx+b, Where m is slope of a line and b is y-intercept of a line.

Finding slope Intercept:

When two points are given, we can use the following formula to find the slope intercept form of a line,

(y-y1)=m(x-x1), where m is slope,(x1,y1) is one point in the line

The slope m can be obtained by using the following formula,

m= (y2-y1)/! (x2-x1), here (x1, y1) and (x2, y2) are the

points in a line or segment.

Or

y-y1/y2-y1=x-x1/x2-x1

Hope you like the above explanation. Please leave your comments, if you have any doubts.

slope intercept form

Rating Climbs: a simple formula

Last post I reviewed some existing ratings for climbs. All fell short. With this in mind, I propose my own rating here.

First, a quick review of my rating philosophy:

1. For simplicity, the rating should be based on net climbing and distance.
2. For sufficiently gradual grades, the rider is assumed to be able to shift to remain in a comfort zone on the climb, and difficulty is then proportional to altitude gained.
3. Beyond a certain grade, climbing becomes much more difficult. It may be possible to construct bicycles which can climb steep grades relatively easily, but the rating is designed for a "typical" fit rider on a typical racing bicycle.

From the description, an obvious candidate for the rating is immediately self-evident for fans of polynomials:

rating = net climbing × (1 + [K × climbing / distance]^N)

The only question is then: what value of K, and what value of N?

First, K: K is the distance / climbing at which a climb is twice as steep as it would be were it more gradual, neglecting issues of added distance traveled (which we're not including in "climb difficulty"). When I'm riding, personally I find "really steep" kicks in at around 12%. Think Metcalf at this past Sunday's LiveStrong Challenge. But the key is that climbs with a high average grade typically vary a bit, or even more than a bit, about that average. So a rock-steady 12% average might be less difficult than the "typical" 12% average grade, which has sections at 15% or more, and others at a more modest (but still steep) 7%. So after playing around with ratings a bit and looking at climbs I know well, I determined a rate of climbing of 10% was a good number to use here. In other words, K = 10.

Next, there's the issue of N. N = 1 reduces to the formula used by Summerson (for infinite K). Honestly I don't think that does justice to really steep climbs like Filbert Street in San Francisco. Filbert gains only a bit over 20 meters, but it's a lot tougher than a 40 meter climb at 15%. So next I tried N = 2. That seemed to work well. N = 3 really kicks in the difficulty at steep grades, but didn't do enough for moderate grade roads.  To be honest, I was going to pick N = 3, but after experimenting with some local climbs, I went back to N = 2.

I plot the formula's result for grades up to 30%. Note this is difficulty per unit climbing, not unit distance traveled. To convert to grade you can use high school trigonometry:

grade = (climbing / distance) / √1 - (climbing / distance)²,

or equivalently

climbing / distance = grade / √1 + grade².

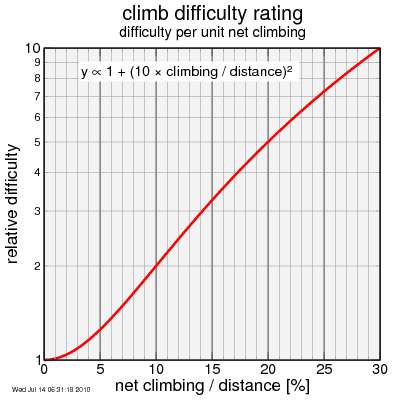Climbing difficulty per altitude gained
This seems to capture things fairly well. It says Filbert Street, the stiff portion of which gains around 18 meters @ 32% actual grade, corresponding to climbing / height = 30.5%, is equivalent to a 5% climb gaining around 150 meters. Well, difficulty on such a steep climb is hard to assess (for example, I might personally find 35% unclimbable), but for a quick-and-dirty rating, not too bad.

So there it is: my proposed formula for ranking the diffulty of climbs:

rating = net climbing × (1 + [10 × climbing / distance]²)

There's still one open question, however: how do I define a climb? Answer: a "climb" is a segment of road which has a higher climbing rating than any overlapping segment of road. What this implies is no "climb" should be rated lower than any subset of that climb. So suppose a climb starts gradually,then is steep for awhile, then levels out, like Metcalf Road.    One should be careful to consider using the steep portion rather than the absolute endpoints of the altitude-gaining segment for the rating.  More on that when I show some examples, but this is a bit of a point of weakness in the rating scheme versus one which used a detailed profile of the climb.  I'll make an attempt at such a rating system in a future post.

simple discount formula

Goodbye

I'm closing Restraint of the Heartless now.

I think now you deserve to know the meaning of "Nulono".

In Esperanto:

• "nul" is the word for zero.
• "-on-" is the suffix for creating a fraction ("kvar", meaning four, plus "-on", plus "-o", makes "kvarono", a fourth or a quarter)
• "-o" is the standard grammatical ending for nouns

Thus a "nulono" would be a "zero-th", or one divided by zero.

Now, division by zero is impossible (as far as we know in 02009), and would have some very serious implications if it was possible. Consider the expression a=b, where a and b can be any numbers. Let's say, for the sake of discussion, that a=2 and b=3002.

• 0*2 = 0
• 0*3002 = 0

By the reflexive property, 0=0.

Because 0*2 and 0*3002 are both equal to zero, we can substitute them in as such:

• 0*2 = 0*3002

So, by the multiplicative property of equality, if divide both sides by zero (multiply them by one "nulono"), we will arrive at an equation that still holds true.

Thus:

• (0*2)*(1/0) = (0*3002)*(1/0)

or

• (0*2)/0 = (0*3002)/0

Simplifying, we get:

• 2 = 3002

This exact same procedure works with any two numbers. Thus, the existence of 1/0 would make any number equal to every other number. Numbers, thus, would be completely meaningless, and the entire field of mathematics would come crumbling down.

What doe! s this h ave to do with me, you ask?

Yes, I am an atheist (in fact, I am an antitheist). I am also a liberal (in fact, I'm a communist). I am also a feminist (In fact, I support the Equal Rights Amendment*). I am also pro-gay. I am! also in favor of helping those in need. I am also pro-science.

Yet I am also pro-life.

I make many people's stereotyping world-views crumble to the ground, just like 1/0 would do to mathematics. I chose "Nulono" because I pretty quickly decided "Cde. Oxymoron" was setting me up for trouble.

*, though equal prote! ction is already in Amendment XIV, so it's technically redunda! nt.

reflexive property

Quadrilateral Practice

Test your knowledge of quadrilaterals!




Homework:
18.3 Quadrilaterals- both sides all
Reading- Read In the Days of King Adobe and complete Think About It questions. Complete workbook pages 126 & 127 in reading workbook.
Complete Blue Math sheet for tomorrow.
Phy. Ed. tomorrow.

quadrilaterals pictures

Finding better explanations

Another advantage for individual students taking math tutoring sessions

Recently, one of my students told me:

“I like your lecture style better than my professor’s. You have a much better way of explaining the subject. He just starts doing problems, and that’s it. Last time he was having a hard time explaining how he was using the absolute value to solve a problem. We were all confused about it, nobody was understanding what he was doing.”

Sometimes when you are studying math, and you see a topic for the first time, you struggle to understand it, and you work out examples until you find a way to get it. Then if you are a teacher, and you only have that one way of understanding the subject, you go out teaching it that way, and som! etimes you confuse all of your students.

Some teachers care a lot about their students understanding their lectures but some other teachers do not care that much. Sometimes they think: “Well, if they don’t get it, though luck.” However, teachers who care about their students understanding the subject, they spend a lot of time thinking up alternative explanations, or better examples, or better ways to illustrate what’s happening.

I remember a few times (years back when I was a teacher) I felt kind of depressed, disappointed, or frustrated at the end of a lecture because I couldn’t find a way for my students to understand what I was trying to explain. Then, afterwards, I would spend hours, days, even weeks sometimes looking for better ways to explain a particular topic, and the next time I taught that course I was able to explain those topics much better.

I noticed when I started private tutoring, that really sped ! up the process for me, of finding better explanations, because! sitting with students one-on-one, and taking the time to go in depth and in detail with them over their doubts and questions, many times I was able to discover exactly how my students in class were looking at specific problems.

That allowed me to discover faster the reasons why they were not understanding a subject, or why some of my explanations were not working. By tutoring individual students, I was able to find a lot faster a lot more alternative ways of explaining subjects when my students in a large class felt the need for those better explanations.

Tutoring individual students has helped me to focus on finding the best way for each student to understand a given subject, rather than focusing only on covering the whole subject fast in front of a big class.

online math tutoring

Back To School Meeting Update

Hosted by 4-H & Polk Christian Home Educators

4-H Homeschool
Outdoor School
September 20-22, 2010
Oregon 4-H Center

The 4-H Homeschool Outdoor School is a program sponsored by Polk County 4-H and Polk Christia! n Home Educators and is open to all youth in grades 5-8.

(We will be having homeschooled high school age youth to serve as counselors. If you are interested in counseling, contact us.)

The program is designed to give youth hands-on outdoor learning experiences with natural science, pond study, forestry, outdoor cooking, leather craft, wind energy, archery, animal habitat, survival skills and more. We will have featured presentations and campfire activities. Free time activities include canoes, swings, crafts, archery, soccer and more.
Camp participants will stay in Cottages that have four bedrooms, each containing two sets of bunk beds with mattresses. The cottages have a common area and bathrooms with private showers. Cabins may also be used. This beautifully wooded location is just 6 miles f! rom downtown Salem. http://www.oregon4hcenter.org/
Cost for the overnight camp is $35 per youth/adults if registered and received by September 13^{th.
Additional $10.00 late fee added Sept. 14th and after.
Scholarships may be available upon request.
Monday – Check-in/Registration 10:00-10:30, Camp begins @ 10:30am
Wednesday – Pick up @ 2:00pm
Additional information and registration:
http://extension.oregonstate.edu/polk/camp
For Questions about the camp contact:
Judi Peters, Polk 4-H Youth
503-623-8395 or 503-931-2578
Email: J! udi.peters@...}

odysseyware answers

Triangle Inequality

Activity
Take broom sticks of different lengths.
(Say, 4cm, 7cm and 13cm)

Can you make a triangle using these sticks?
Now, try to find a relation between the largest side and the sum of the remaining two.

Repeat this by taking few more sets of broom sticks.

What do you notice?

Based on your observations, write a conjecture about the relationship between the sum of the measures of the two sides of a triangle and the measure of the largest side of the triangle. Provide a reason for your conjecture.

Thinking questions?

Two sides of a triangle are 6 cm and 10 cm long. Determine a range of possible measures for the third side of the triangle.

Is it possible to have a triangle such that the sum of the measures of the! two sides is equal to the measure of the largest side? Provide a convincing reason for your answer.

my maths answer sheet

Math tutoring for low-achieving students

Ronnie Karsenty has written an article entitled Nonprofessional mathematics tutoring for low-achieving students in secondary schools: A case study. This article was published online in Educational Studies in Mathematics last week. The project that is reported in the article is part of a larger project (SHLAV - Hebrew acronym for Improving Mathematics Learning). The research questions in the study are:

1. Will nonprofessional tutoring be effective, in terms of improving students' achievements in mathematics, and if so, to what extent?
2. Which factors will be identified by tutors as having the greatest impact on the success or failure of tutoring?

Here is the abstract of the article:

This article discusses the poss! ibility of using nonprofessional tutoring as means for advancing low achievers in secondary school mathematics. In comparison with professional, paraprofessional, and peer tutoring, nonprofessional tutoring may seem less beneficial and, at first glance, inadequate. The described case study shows that nonprofessional tutors may contribute to students' understanding and achievements, and thus, they can serve as an important assisting resource for mathematics teachers, especially in disadvantaged communities. In the study, young adults volunteered to tutor low-achieving students in an urban secondary school. Results showed a considerable mean gain in students' grades. It is suggested that affective factors, as well as the instruction given to tutors by a specialized counselor, have played a major role in maintaining successful tutoring.

math tutor online

Have questions about math problems

Have questions about math problems, get help on this website. You will learn the toughest questions with the easiest way to solve it!!

how to solve math problems

Spring is Springing with Recipe for Watermelon, Feta, and Arugula Salad (ÎÏοÏεÏή ΣαλάÏα με ÎαÏÏοÏζι, ΡÏκα και ΦέÏα)

Friday felt like the first true day of spring. The sun was shining, and I could almost feel the trees and plants waking from their winter slumber.

Oh sure, there’s still snow on the ground, the trees are bare, and the temperatures are still in the low 30s at night. But the days are gloriously long, 13 hours of daylight and rising, and the sun’s warmth is finally breaking through.

I grabbed a knife and bag and unsuccessfully went hunting for the first dandelions of the year. Although they weren’t up yet, I did see tiny red leaves of garden sorrel poking through the dirt. Primroses and leopard’s bane are up and growing rapidly.

I wore boots and a wool coat for my Friday shopping. After the first stop, I dumped my coat in the car and basked in being able to walk around unencumbered. I saw women in sleeveless tops and men in shorts. It may be cold according to the thermometer, but Alaskans respond to the first sunny spring weather with outbursts of irrational exuberance.

The grocery store’s produce aisle was stacked high with reasonably priced melons, reflecting South America’s seasonal bounty. I couldn’t resist a cut of juicy red watermelon, and decided to make a Watermelon, Feta, and Arugula Salad and pretend the snow was long gone.

The salad is one of my favorite dishes at Kuzina, a restaurant near the Ancient Agora archeological site in downtown Athens. Kuzina has an interesting menu, a very competent chef, and specializes in creative Greek cuisine.
We were last at Kuzina in September. My brother Bill and ! sister-i n-law Tommie had come to visit us in Greece; we met them in Athens before going to the island. It was great fun to show them around the city, and see it fresh through new eyes. The day we went to Kuzina, the four of us had spent the morning walking and walking through the fascinating Athenian streets.

One of my favorite things about Athens is the wonderful graffiti art painted on walls of abandoned and inhabited buildings alike. Here are some examples of the street art we saw on that sunny September day with Bill and Tommie:

By lunchtime, we were ready for something cool and refreshing, so headed over to Kuzina and ordered watermelon salads. It was the perfect lunch for a perfect day.

Wa! termelon, Feta, and Arugula Salad (Î"ροσερή Σαλάτα! με Κ αρπούζι, Ρόκα και Φέτα)
Adapted from Kuzina Restaurant, Adrianou 9 (Thissio), Athens, Greece
This salad is simple to make, and the arugula and balsamic make it special. The keys are cutting the watermelon thick enough to stand on edge, and finding firm feta that can be cut into large flat pieces. It’s also important to use good quality traditional balsamic vinegar. If you can’t find good balsamic, you can replicate its flavor by enhancing commercial balsamic with a little brown sugar. I use a ratio of 1 tsp. brown sugar per 5 tablespoons of commercial balsamic.

Watermelon
Feta cheese
Arugula
Best quality balsamic vinegar

Cut the watermelon into 1” slices. Cut off the rind, and cut the flesh into sharp triangles (use the watermel! on trimmings for another purpose). I try and remove the seeds for ease of eating, but it’s not necessary to do so.

Cut the feta into slices and then into the same shape triangles as the watermelon, but slightly smaller. I cut the feta smaller than is shown in the picture because doing so creates a better balance of ingredients.

Wash, clean, and dry the arugula.

Arrange the watermelon and feta slices as shown in the above photogaph, and fill the center space with arugula. Drizzle balsamic vinegar over everything, and serve.

~~~~~~~~~~~~~~~~~~~~~~~

Other Interesting Salad Recipes

Beet, Fennel, and Leek Salad with Lemon-Ginger Dressing (Παντζάρια, Μάραθο και Πράσο! ΣαλΠ¬Ï„α με Πιπερόριζα Σάλτσα)
Beet and Red Pepper Salad (Παντζάρια Σαλάτα με Κόκκινες Πιπεριές)
Fennel-Preserved Lemon Salad with Preserved Lemon Aioli (Σαλάτα με Μάραθο και Λεμόνια)
Grilled Radicchio and Arugula Salad with Parmesan Shavings (Σαλάτα με Ψητό Ραδίκιο, Î! ¡ÏŒÎºÎ±, και Παρμεζάνα)

To find more salad recipes, Food Blog Search is a great tool.
~~~~~~~~~~~~~~~~~~~
This is my entry for Weekend Herb Blogging, hosted this week by Susan from The Well-Seasoned Cook.

how to cut a watermelon into triangles

Tangrams Sample Projects

This year, I am going to try to be good about scanning in stuff that my kids have made, so you can see how a project is intended to look / work. :) I love it when other teachers post pictures or videos of what goes on inside the classroom. It makes their lessons seem so much more real!

Here is one. The tangrams project was super fun, for both me and the kids. In the process, we learned how to find angles using adjacent angles in a diagram, how to find angles inside an isosceles angle, how to use Pythagorean Theorem to find diagonal lengths, how to find lengths of sides that "stick out" in a picture, and how to combine / simplify square roots and whole numbers! Wow. So much math in 2 or so days of class time. :) :) And the kids loved the puzzly parts of the project, piecing the tangram pieces together to make the silhouettes. Some kids also took the initiative to create their own designs and to find additional perimeters, which was really fun for me to grade!

Here are the scanned images of a couple of example projects. They look lovely in person, but the math work is in pencil (and some of the colors are also light), so the scanner unfortunately doesn't pick it up all too well. If you zoom in, you can see the math that they wrote next to the diagrams.

Entire project from Kid #1:




Parts of project from Kid #2:

bar graph template for kids

Making the fractions in a proportion

"How do you know how to make the fractions in a proportion?
When making them, how do you know where each number goes making the fraction, like which ones go on top of the fraction?"

Well, actually you can choose which quantity will go on top; the proportion WILL work either way!

But, sometimes people are used to always putting certain quantity on top and certain on the bottom. For example, if the question is about speed and the unit is "miles per hour", that tells you that miles go on top, and hours on bottom, because "per" means division (the fraction line).

However, you could still solve the proportion by putting hours in the numerator of the fractions and miles in the denominator, and the calculation will turn out alright.

Or, if the question is about "dollars per pound", then dollars go to the numerator and pounds in the denominator.

Let's look at this problem for example:

A car drives on constant speed. It can go 80 miles in 90 minutes. How long will it take for it to travel 100 miles?

You can make both fractions to be

miles
-----------
minutes

OR

minutes
------------
miles

Let's try the first way:

80 mi           100 mi
--------  =   ---------
90 min            x

To solve, cross multiply and you get 80x = 100 * 90, and then x = 900/8 = 112.5 minutes.

The other way it will be

90 min         x
--------  =  --------
80 mi         100 mi

To solve, cross multiply and you get 80x = 90 * 100

You see, the final equation ends up being the same, no matter which
quantities were on top of the fractions! .

HOWEVER, one way is wrong: that is if you but "mi! les" on top in one
fraction, and "minutes" on top in the other... then you'll get it wrong:

90 min        100 mi
--------  =  -------
80 mi         x min

=> 90x = 100* 80 (WRONG)

math proportion

Retirement Calculator Evaluation - Vanguard

Overall, I thought the Vanguard Retirement Calculator was a reasonably accurate estimator for how much is needed. It takes salary growth (due to inflation), social security payments, and life expectancy during retirement into account.

However, if one is more than 10 years from retirement, you may need to make an adjustment to one’s estimated salary. The calculator does not account for the possibility that your salary may grow faster than inflation during your early working years – e.g. due to promotions or job changes. For those that are 10 or more years from retirement, it may be necessary to project what your! future salary may be and put the present value in the salary column. (For specifics on this economic-speak, see example #2 below.)

This calculator asks for the following information:

1. Household Income
2. Percentage of Income Needed after Retirement
3. Social Security Benefts
4. Annual Pension Benefits
5. Current Savings
6. Annual Retirement Savings Contribution
7. Annual Investment Returns
8. Years Until Retirement
9. Years in Retirement

After filling out the information, the calculator lets one know whether you have sufficient savings or the amount that one needs to save before retirement.


Example 1 – Will B. Retired is a 64 year old that will retire next year. Here is his information.

1. $50,000 total income
2. 100% income needed in retirement
3. $25,560 Social Security (used 55 year old numbers)
4. $20,000 annual pension
5. $1! 0,000 savings
6. $5,000 savings per year
7. 8% savin! gs retur n in retirement
8. 1 year until retirement
9. Life expectancy – 95, i.e. 30 years in retirement


Income needed for retirement. $52,000 in year 1. The calculator shows that Will’s retirement income will be $48,786. Most of it is covered by Social Security and his pension. This situation is acceptable since Will is so close to retirement. However, the calculator recommends Will needs to save about $185,000 more to account for the possibility of higher inflation. Thus, Will savings is currently short and should work longer before retiring.

Example 2 – Em. S. Grad is 35 years old and plans to retire at 65. Em’s information is different that Wills in #3 (social security payments), #4 (assume there are no longer pensions), and #8 (30 instead of 1 year to retirement). In addition, Em expects to retire as a Division Manager, which has a current salary of $150,000.

1. $50,000 total income
2.! 100% income needed in retirement
3. $28,638 Social Security
4. $0 annual pension
5. $10,000 savings
6. $5,000 savings per year
7. 8% savings return in retirement
8. 30 year until retirement
9. Life expectancy – 95, i.e. 30 years in retirement

Amount needed for retirement: $1,266,596 to enable $162,000 per year of retirement income. And the calculator judges that Em is on track to provide $152,036 per year, assuming Social Security payments increase at the rate of inflation. Thus, Em will need to save about $1250 more per year to reach his goal.

However, the calculator doesn’t account for non-inflation related salary increase. Thus, $1,266,596 should be Em’s minimum retirement savings target.

To account for a higher salary due to promotion or job change, I recommend that Em should use the present salary of the position he expects have in the future. For example, if Em expe! cts to be a division manager when he retires, he should input ! the $150 ,000 salary of a division manager today. (For reference, I also changed the Social Security payment to the maximum of $36,864.) With this adjustment, here is what Em would need for a retirement nest egg: $6,708,059. This would represent the high side retirement savings target. For reference, this number is close to the T.Rowe Price calculator estimate of $7,427,816, which did not include Social Security payments.

Disclaimer: Examples are illustrative purposes only. Your results will vary with different inputs and assumptions. As with all retirement calculators, please consult with your financial advisor before taking any actions.

Photo Credit: morgueFile.com, Emily Roesly

5 number summary online calculator

Java : List Prime Numbers between 1 to Given Number

This program find the even numbers between 1 to the number enter by user :

import java.io.*;
class AllEvenNum{
public static void main(String[] args) {

try{

BufferedReader br1 = new BufferedReader(new InputStreamReader(System.in));
System.out.println("Enter a Number : ");
int num = Integer.parseInt(< /span>br1.readLine());
System.out.println("Even Numbers are:");
for (int i=1;i <=num ; i++){
if(i%2==0 ){
System.out.print(i+",");
}
}
}
catch(Exception e){}
}
}

List prime numbers

Lowest Common Denominator (LCD) // Julie's super scribe

My super scribe is about lowest common denominator

What is LCD?
**Lowest common denominator is the least common multiple of the denominators of a set of common fractions.

To find the least common denominator, you have to find the least common multiple.


You have to find ! the lowest common multiple of 4 and six.

To find the lowest common multiple you have to list the factors of 4 and 6

Four: 4 8 12 16 20 24 ... and so on
Six : 6 12 18 24 30 36 ..... an so on

so The lowest common denominator of 3/4 and 5/6 is 12 because thats the least commmon multiple. Its not 24 because 12 comes first.

<--- how to get the numerator.

least common multiple lcm

A METEOROLOGICAL MODEL FOR THE CONCENTRIC CIRCLE SUN SYMBOL IN ROCK ART OF THE AMERICAN SOUTHWEST:

One common theme in the rock art of the American southwest is the symbol of one or more concentric circles, often around a central dot. This symbol of concentric circles has been recognized as a representation of the sun throughout Ancestral Puebloan rock art of the American Southwest.

The pueblo culture is, and has been, constructed around an agricultural tradition based on maize, beans, and squash. The people depended upon their faith and knowledge of the natural cycles of their environment to provide for their families. Many of the petroglyphs and pictographs created by the Anasazi understandably illustrate a concern with the weather, portraying symbols such as clouds and rain. One of the most common weather symbols is the sun, portrayed as one of the variations of the concentric circles theme. As a symbol for the sun, these concentric circles model a specific atmospheric condition, the haloed sun.

Concentric circle sun symbol,
Sego Canyon, Utah.
Photo: Peter Faris, 1980.

Concentric circle sun symbols,
Signal Hill, Tucson, AZ.
Photo: Jack & Esther Faris, 1990.

As the sun moves north of the equator in the Northern Hemisphere summer, the land mass is rapidly warmed. This leads to the development of a low-pressure cell over the arid North American Southwest. Winds follow a pressure gradient from high to low and flow counterclockwise about a low in the Northern Hemisphere, bringing a monsoon flow of moist air from the Gulf of California over Arizona and New Mexico by mid-July, accompanied by afternoon showers and thunderstorms. As the moist air heats up over the desert, it rises and begins to cool with increased altitude. This rising air can reach an altitude of as high as 15 km, forming the thin, sheet like high altitude cloud cover called cirrostratus that often covers the entire sky so thinly that the su! n and moon can be clearly seen through them. Ice crystals in the cirrostratus can refract the light passing through them producing a circle around the sun or moon known as a halo. The most common halo is the 22º halo, a ring of light around the sun or moon at a radius of 22º, about the distance from the end of the thumb to the little finger on the outstretched arm. These conditions are also often a precursor to oncoming precipitation within a few hours to a day.

Sun with halo, May 19, 201! 0. Photo : Peter Faris, 2010.

Sun with halo, May 19, 2010. Photo: Peter Faris, 2010.

The solar halo illustrated was photographed at my home on the morning of May 19, 2010, and rain began to fall approximately four hours later.

Tawa, Sun kachina.

As a precursor of precipitation a circle around the sun would be of great import to a people dependent upon rain for a successful harvest. Such a case might be expected to apply in the American Southwest where agricultural societies were aware of their almost total dependence upon precipitation for the success of their crops. This possibility is reinforced by the design of the case mask worn by the Sun Kachina (Hopi Tawa Kachina) which is quite clearly circular and is surrounded by a border of black-tipped feathers. In this mask the white body of the feather and t! he ring of their black tips represent the concentric circles a! round th e face of the sun. Thus the haloed sun, which may have originally inspired the concentric circle symbols in Ancestral Puebloan rock art, can still be seen in the Sun kachina mask worn by Puebloan kachina dancers and remains a living factor in their beliefs.

concentric circle art

Several Circles (1926) by Wassily Kandinsky and the Golden Rectangle

Golden Rectangles

Wassily Kandinsky (16 December 1866 - 13 December 1944) was a Russian painter, printmaker and art theorist. One of the most famous 20th-century artists, he is credited with painting the first modern abstract works.
Click the figure below to see the interactive illustration of Several Circles (1926) by Wassily Kandinsky and the Golden Rectangle.


Read more:
Several Circles by Wassily Kandinsky and the Golden Rectangle

geometry circles

Problem 455: Rhombus, Inscribed Circle, Angle, Chord, 45 Degrees

Geometry Problem
Click the figure below to see the complete problem 455 about Rhombus, Inscribed Circle, Angle, Chord, 45 Degrees.


See also:
Complete Problem 455

Level: High School, SAT Prep, College geometry

chord circle

Just an Average Point

Somewhere back in Alg I, we introduce the midpoint, and maybe some bright kid notices that the midpoint of (2, 7) and (6, 9) is just (4, 8); which is just the average of 2 and 6 followed by the average of 7 and 9; just average the x-values and average the y-values

Later in Geometry, we introduce midpoints all over the place, midpoints of a segment, as one end of the medians of a triangle, or as a point on the perpendicular bisector, but it is almost always in an abstract approach and they never actually have to ferret out the coordinates, so that seldom gets reinforced. I think that is a shame, because in the same course, we get another nice opportunity to introduce the 2 dimensional equivalent. One of the beautiful geometric ideas that still persists in a few geometry classes is that the three medians always intersect in a point. The point is called the centroid*, and sometimes the center of gravity. (Some teachers like to have students make triangles out o! f cardboard and after they find the centroid the students can cut it out and balance the cardboard triangle on a pencil tip.) If you use an interactive geometry software package, like sketchpad, you can actually construct the triangle and its medians, then grab a point and drag it around and see that...wow! no matter how you alter the shape of the triangle, the three medians still intersect in a single point. If you don't have the software to play with on your on, you can open a java applet I made here and click the mouse button on any of the triangle vertices and move them freely.

But almost no geometry class I know of goes on to show that the point is really sort of a "midpoint" of the triangle, and like the midpoint of a segment, it is just an "average" point. The x,y coordinates of the centroid are just the average of the x-coordinates of the three points followed by the average of the y-coordinates.
! If, for example, we had triangle ABC with A=(1, 2); B= (5, 11! ) and C = (9, -1) then the medians will intersect at the point where x= (1+5+9)/3=5 and y= (2+11 - 1)/3 = 4; or more simply at the point (5,4)
About this time of year as I am introducing my pre-calc class to the beauty of three dimensional analytic geometry, I dust off their memory of this little jewel from when I taught it in Alg II, and then we extend it to show it works with triangles in three-space. This requires them to a) Find the midpoints of the sides; b) write the equation the medians in the space triangle; c) find the intersection of two vector lines in space; (d) and then confirm that that point is also on the third l! ine; and finally e) insure that it is indeed the average of the relative coordinates. I think it is a pretty good illustration of the power of the linear algebra they are learning.

As a reward, I give them a discovery lesson on tetrahedra... we talk for a minute about the difference between a two dimensional object in three space (A triangle with (x,y,z) coordinates for the points) and a three dimensional object (like a cube) . I bring out a large cardboard model of a tetrahedron (triangle based pyramid) and hold it in front of me..... and I begin to wonder aloud..." This is sort of like an extension of a triangle in three dimensions.... so what would be like the medians of a triangle in this object?"
Frequently the first guess is a line from a vertex to a point which is the "face-center" or centroid. I usually channel them (or prompt them if needed) toward this idea. "Wouldn't it be wonderful", I add, " if there was something like the centroid ! for the tetrahedron; where all those lines would intersect." ! By now t hey suspect that there is, and perhaps with some fear as they realize that they are about to be challenged to find one, or worse, prove it is always true.

With much the same vector approach as before, I pass out some cards with a set of four points in space (carefully chosen to make the work a little less messy than it might be), and they find centroids of the four faces, hopefully using the "average point" method. Then they must write vector equations of the four lines which I call "medial" lines that run from a vertex of the tetrahedron to the centroid of the opposite face. Finally I suggest that they solve the intersections of the four medials in sets of two, and behold that the two solutions are the same point; all four lines intersect in a single point.

Then I ask, "What is the quickest way to find the midpoint of a line segment?" "Averages", they shout.

"What is the quickest way to find the centroid of a triangle?" "Averages", some reply, but others already have anticipated the next question, and have started to calculate the average of the four x values.... could it be?

As a finale I point out that there is a pattern in the division of the segments in each of the cases..
The midpoint divides the line segment (a one space object) into a ratio of 1:1
The centroid divides the segment of a triangle (a two space object) into a ratio of 2:1
The center of gravity of a tetrahedron ( a three space object) divides the medial segments in a ratio of 3:1

Just another "average" day in mathematics class.

If you want a little more about centroids, see my web page article.


*There are three common "centers of gravity" that are studied in math, science and engineering. The most common in math is the center of masses loc! ated at the vertices of a polygon. This is more common because! the oth er two cases can be reduced to a variation of this approach. It is this case of point masses at the vertices that I mean when I use centroid or center of gravity in this note, unless otherwise stated. A second approach is to treat the area of the polygon as if it were a sheet of uniform density. The third, and least common, approach is to represent the sides of the polygon as wire rods of uniform density.

Most students are first introduced to the terms above in reference to a point in a triangle. Since the center of masses at the vertices in a triangle give the same point as a uniform sheet, they are often confused about the various distinctions. The three centers of gravity are usually different points in other non-symmetric polygons. It is this point, the center of balance for the uniform sheet and also of point masses at the vertices, that is almost universally referenced as the centroid of a triangle.

centroid of a triangle

Free algebra worksheets

Usually algebra textbooks provide lots of problems to practice the algebraic concepts and techniques, but some of you may still benefit from resources for free (or mostly so) printable algebra worksheets. Please see the list below, which I've originally compiled for my HomeschoolMath.net site.

Algebra worksheets

Worksheet Builder
Great and free worksheet maker software with nearly 7,000 built-in algebra and geometry questions.
www.jmap.org/JMAP_WORKSHEET_BUILDER_INSTALLATION_FILES.htm

Free Algebra Worksheets from KUTA Software
Free worksheets (PDF) for equations, exponents, inequalities, polynomials, radical & rational expressions and more.
www.kutasoftware.com/free.html

AlgebraHelp.com worksheets
Interactive worksheets that are checked online for most algebra 1 topics.
www.algebrahelp.com/worksheets/

Math.Com algebra worksheets generator
Generate worksheets for: linear equations, systems of equations, and quadratic equations.
www.math.com/students/worksheet/algebra_sp.htm

LessonCorner worksheets
These free worksheets include a few topics such as calculations with polynomials, factoring, and graphing lines.
www.lessoncorner.com/worksheets/

Algebra Fun Sheets
Worksheets that integrate algebra skills with fun activities including sudoku, word finds, riddles, color patterns, crosswords, games, matching cards, etc. A subscription is required.
www.algebrafunsheets.com

About.com Algebra Worksheets
An assorted collection of free algebra worksheets and answers. These pages are not very well organized, but they have lots of worksheets.
math.about.com/od/algebraworksheets/Algebra_Worksheets.htm

Algebra Worksheets from MathWorksheetCenter
Lots of worksheets for over 100 algebra topics. A few are free; most are accessible only by one-year a subscription.
www.mathworksheetscenter.com/mathskills/algebra/

A few fun algebra worksheets
These are for graphing linear equations and linear inequalities.

Online Math Work
Free multiple-choice worksheets for pre-algebra and algebra 1 topics. You can do them online, or copy to a word processor to print.
www.mathonlinework.com

Lastly... my own algebra worksheet collections, which aren't free but there are many free samples:

Math Mammoth Algebra 1 Worksheets Collection
A two-part collection (A and B) of 137 quality algebra worksheets covering all the topics in a typical algebra 1 curriculum. These worksheets are hand-crafted and contain lots of word problems and other variable problems. Free samples available. $11.50.
www.mathmammoth.com/worksheets/algebra_1.php

algebra answers

TSA AND FAA JOINTLY ANNOUNCE NEW SECURITY PROGRAM FOR AVIATION

The tragic event of the deranged and frustrated Piper pilot (I learned to fly in a Cessna, so I think this applies to ALL Piper pilots. Okay, okay, just kidding!!) that went off his rocker last week, and crashed into the IRS building in Austin (sadly killing an employee) has no doubt got us all thinking 1) about the family of the IRS employee, and 2) about the family of the deranged lunatic. Our sincerest heartfelt sympathy goes out to those families.

We shall continue to reflect with sorrow over the sad consequences that childish and sad act of selfishness and evil had for the loved ones left behind. And, as "critic"-al thinkers, I have no doubt that most of us are also wondering what the longer term consequences to the! General Aviation community might be, and how that act of deviance, might result in some further deviation from the norm we used to know in pre- 9-11 days, particularly regarding smaller airports where many of us hang out to watch planes and cheer the marvel of flight. (And drink beer when no one is watching, judging from the empties in the parking lots...). Or even perform delightful feats of challenging the laws of gravity- and probability, in my case.

(At least according to the many unkind, and unsolicited, critiques of my landing "style". No doubt, most are from jealous Piper enthusiasts, who are envious of a 172's ability to gracefully bounce about half a wingspan, instead of rather blandly plopping onto the runway- much like rather uncerimoniously dropping a wet towel. In stark contrast to the playful and spirited response of, say, dropping a golf ball onto a concrete sidewalk. From a third story window or so).

While we continue to grieve for the! affected families of last week's tragedy, we also contemplate! what co ming actions might be taken in a constructive way, and perhaps well intentioned, but not quite so productive ways. One of our blog's great thinkers (and satirist/parody-ists) has put his formidable powers of analysis towards what might be the resulting aftermath of recent events.

Without further ado, here's our friend Black Tulips's first (of many, I hope) return engagement as a "headliner" (I suppose I give the Cessna's headliners a pretty good work out) on A.C. & E. :

February 20, 2010 – Washington, DC

The world still reels from the shock of Texas pilot Joseph Stack flying his Piper Cherokee into a Federal office building in Austin. The! man’s grudge against the IRS ended in a fiery suicide attack. The Federal government has scrambled to react to this homegrown tragedy which some consider a domestic terrorist act. The Transportation Security Administration (TSA) is currently without a leader so Janet Napolitano, Secretary of the Department of Homeland Security, has stepped into the breach. “This is Nine-Eleven all over again except the terrorist had lighter skin and no accent”, she said. “I told you this was going to happen. The Obama Administration gave business and general aviation one chance too many.”

Napolitano continued, “I am pleased to announce today the formation of the Total Air Marshal Program (TAMP). There are 240,000 active general aviation aircraft in the United States and an Ai! r Marshal will be assigned to each aircraft. With over 600,000! active certificated pilots in the United States we can’t have an Air Marshal for every pilot – but we can have one for every plane.”

At this morning’s press conference she turned to Rahm Emmanuel, White House Chief of Staff, who said, “We are pleased with this rapid reaction to a domestic terrorist threat. We can’t let some retard in a bug smasher hold up tax collections in Texas. President Obama considers this an example of his dynamic and flexible Stimulus Package. Now there is a demand for 240,000 new jobs that weren’t there yesterday. Hotels and restaurants around the country will benefit from the Air Marshal’s spending.”

Emmanuel added with emphasis, “This should also make the Second Amendment folks happy as the Government is going to p! urchase a quarter million handguns. Nine millimeter is the preferred caliber as it will minimize collateral damage to pressurized aircraft.”
Next Randy Babbitt, Administrator of the Federal Aviation Administration (FAA), took the microphone, “We realize that some will consider this an inconvenience and overreaction. In order to ease the application of this rule we made several important changes to the Federal Air Regulations (FARs). No longer will there be a limit on the number of crew or passengers in one seat belt at a time – independent of age and weight. Also you can expect a new set of pages for your Pilots Operating Handbook (POH). Depending on runway length and density altitude, pilots need not consider the addition weight of the Air Marshal and their luggage. In other words aircraft owners can add about 250 pounds to takeoff weight without regard to center of gravity.”

Secretary Napolitano offered concluding remarks, “We r! ealize s ome will consider this expansion of the Air Marshal program an intrusion. For that reason the Federal government is seeking wide diversity in the Air Marshals. For the older family-oriented flyers we will offer retired law enforcement officials. For the younger and more adventurous we have several possibilities. Several of Tiger Woods’ mistresses have signed up and are in training. However we do have a shortage of gay, lesbian, bisexual and transgender Air Marshals… especially the latter. I encourage all who have an interest in joining the rapidly growing Total Air Marshal Program for a bright future in the United States Government.”

Thanks BT- it's a great piece, with of course no disreverence for the deceased whatsoever- and I laughed harder than those whiny Piper guys who watch me land!

Analytical cartesian coordinate system

Converting Mixed Radicals To Entire Radicals, Adding/Subtracting Radicals

Today's Assignment:
page 14 -- finish yesterdays assignment questions 41-100, then do 101 - 135 all and 137-149 odds.

THIS IS FOR HOMEWORK. THERE WILL BE A QUIZ ON THIS TOMORROW (Thursday)

subtracting radicals

A Guide to Earn GOLD

If you are tired of trying to figure out who to trust, if you are tired of trying to figure out what voice to listen to for guidance, if you are tired of trying to be in the right place at the right time, whatever that means. Explore the world and see all the wonders. Give gold a try. It sounds like it may be right for you. Over the last 10 years gold has outperformed virtually every other investment out there. From stocks to bonds to real estate, there has not been any other investment that not only provides an above average return but also the feeling of security associated with just leaving your money in a savings account. Gold prices here are much worthy. You are assured of the quality and in time the prices will become higher and higher.

Gold is precious, though this time it is not that popular compare to real estate business. Bu! t it is a good business venture; you can earn much on this kind of business. Gold price will eventually go higher and higher as time pass by. A very good investment. Here are the The current five participants who fix the price of gold:

• Scotia-Mocatta - successor to Mocatta & Goldsmid and part of Bank of Nova Scotia

• Barclays Capital - Replaced N M Rothschild & Sons when they abdicated

• Deutsche Bank - Owner of Sharps Pixley, itself the merger of Sharps Wilkins with Pixley & Abell

• HSBC - Owner of Samuel Montagu & Co.

• Societe Generale - Replaced Johnson Matthey and CSFB as fifth seat

In our world right now, it’s always ! right to find something you can have in the future. For me GOL! D is the answer.

free algebra 2 answers

Creating Creativity

Earlier in the month, Tony Schwartz, on the Conversation (one of the Harvard Business blogs) wrote a piece  called Six Secrets to Creating a Culture of Innovation.

It's geared towards those running a business, primarily, but I thought it might be interesting to consider how a loan wolf artist like myself might use the 'secrets.'

The first secret is 'Meet people's needs.'   Well, that's something I have no problem doing: if my inner man says, in the middle of writing something, I'm hungry, I send him off to the kitchen (which is conveniently placed a couple of metres away from my computer).   He can make as many cups of tea or coffee as he likes in a day - or finish off that fruitcake someone obligingly gave me...him.   If my inner man has unmet needs, I know about them pretty quickly, as you can imagine.   I can't always settle them immediately, (especially if the fruitcake was finished the day before) but I do my best.

The second secret (how can these be secrets if he's telling us them?) is 'Teach creativity systematically.'   According to Schwartz there are five well-defined, widely accepted stages of creative thinking: insight, saturation, incubation, illumination, and verification.   I read the blog post the link in the previous sentence takes you to (it's very irritatingly bringing up some oddball codes on my browser) and I don't particularly disagree with these steps.   Although when she (someone called simply, Maria) says, "The first stage of the c! reative process is finding or formulating a problem. The tricky part about this stage is that it requires creativity in itself," I kinda feel that there's a bit of a catch 22 in there somewhere.   However, these stages are worth considering - once I've dealth with one of my inner man's unmet needs.

The third secret is to nurture passion.   I have to be excited about what I'm creating.  Don't give me some mundane work to do; my inner many won't stand it.  He'll hive off to the kitchen again.

This ties in with the fourth secret: make the work matter.  There's no point giving me a job writing about cashmere mittens for women if I don't have some excitement about aforesaid cashmere mittens - or about women, if it comes to that.   But if you can get my creative juices going when it comes to cashmere and mittens and women (and not necessarily in that order), you're on the way.

Provide the time.  This is the penultimate secret (another secret Mr Schwartz doesn't mention is include slightly more obscure words in your blog posts).   I try to give my creative person all the time in the world.   What does he do with it?  Fritters it away on Twitter or Facebook or writing blog posts of an inane nature, or checking his emails every few seconds, or playing another round of Scrabble online or seeing if anyone's paid him for anything in the last week/day/hour/second.   I can be a slightly tetchy boss at times.

Finally we have: Value Renewal.  Mr Schwartz says that human beings are not like computers; they can't be left on day and night flicking meaningless screen savers across their faces.   Human beings need to expend energy and then relax.  Expend and relax.  In the relax stage they recover their creative juices and get ready for another hack at the problem in question.   And at the same time, miraculously, while they're whiling away time making the fourteenth cup of tea/coffee, or playing 'fetch' with the puppy, or checking out the Guardian sports videos, all sorts of remarkable creative breakthroughs are taking place.   When that cup of coffee is drunk, or the puppy worn out, or the videos have proved to be not as exciting as the Guardian made them out to be, then you'll find that the brain is just! itching to go, full of new insights, ideas, stuff you can use.  Or not.


Sometimes this creative incubation stage just doesn't get itself going quite as quickly as you'd like, and a whole day, or week or more can be whittled away while the incubation is going on.   However, you can fool the brain by working on some other totally unrelated project in the meantime, and give it a double job to do: incubate on project one and project two simultaneously. 

The brain may happily mix these up - and according to all creative writers this is a good thing.   Just make sure that at the end of the day that project 1 winds up with creative solutions to itself and not to project 2.  Unless your boss also thinks that's a good thing.  

Photo by velo_city on Flickr.com

algebra 2 helper

A Guide to Earn GOLD

If you are tired of trying to figure out who to trust, if you are tired of trying to figure out what voice to listen to for guidance, if you are tired of trying to be in the right place at the right time, whatever that means. Explore the world and see all the wonders. Give gold a try. It sounds like it may be right for you. Over the last 10 years gold has outperformed virtually every other investment out there. From stocks to bonds to real estate, there has not been any other investment that not only provides an above average return but also the feeling of security associated with just leaving your money in a savings account. Gold prices here are much worthy. You are assured of the quality and in time the prices will become higher and higher.

Gold is precious, though this time it is not that popular compare to real estate business. Bu! t it is a good business venture; you can earn much on this kind of business. Gold price will eventually go higher and higher as time pass by. A very good investment. Here are the The current five participants who fix the price of gold:

• Scotia-Mocatta - successor to Mocatta & Goldsmid and part of Bank of Nova Scotia

• Barclays Capital - Replaced N M Rothschild & Sons when they abdicated

• Deutsche Bank - Owner of Sharps Pixley, itself the merger of Sharps Wilkins with Pixley & Abell

• HSBC - Owner of Samuel Montagu & Co.

• Societe Generale - Replaced Johnson Matthey and CSFB as fifth seat

In our world right now, it’s always ! right to find something you can have in the future. For me GOL! D is the answer.

Free online algebra 2 help

Math Mammoth Geometry 2

I have just finished writing the material for Math Mammoth Geometry 2 book. The material in it is suitable for grades 6-7. Download price is $5.80.

The main topics in the book include:

* angle relationships
* classifying triangles and quadrilaterals
* angle sum of triangles and quadrilaterals
* congruent transformations, including some in the coordinate grid
* similar figures, including using ratios and proportions
* review of the area of all common polygons
* circumference of a circle (Pi)
* area of a circle
* conversions between units of area (both metric and customary)
* volume and surface area of common solids
* conversions between units of volume (both metric and customary)
* some common compass-and-ruler constructions.

I've included several complete lessons from the book as samples (PDF). Feel free to download these and use with your students!

Angles in Polygons
Review: Area of Polygons, 1
Surface Area

Besides those, there are two other sample pages:

Area and Perimeter Problems
Basic Compass and Ruler Constructions, 1

What is next?

• See more information
• Purchase a download at Kagi
• Purchase a download at Currclick

geometry homework help free